이름과 다르게 추가 키 값을 삽입하지는 않는다. 그냥 입력한 배열에 있는 숫자들을 두 묶음으로 나뉘어 진다. 왼쪽 묶음은 정렬된, 오른쪽 묶음은 정렬 안 된. 정렬되지 않은 오른쪽 묶음에 있는 숫자들이 하나하나 왼쪽 묶음으로 옮겨지면서 각 정렬된 숫자들을 비교하며 적절한 자리를 잡는다. 물론 처음에 배열 전체가 정렬되지 않았을 초기 때는 둘 째 숫자 array[1] 가 첫 째 숫자 array[0]이랑 서로 비교를 시작하고 나서야 정렬된 왼쪽 묶음이 탄생한다. 말 그대로 array[n]이 array[n - 1]을 계속 비교한다.
내가 방금한 설명을 이해 못 했다면 비쥬얼로 설명하자.
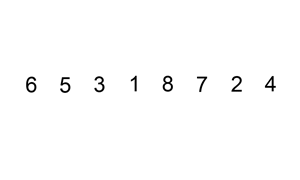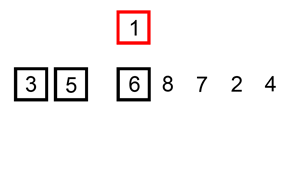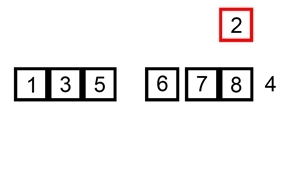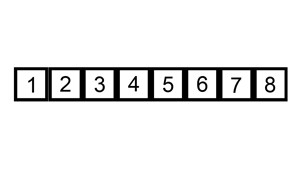
메서드: 네이브 (Naive)
의사 코드는 다음과 같다.
Insertion-Sort(A)
for j = 1 to A.length
key = A[j]
// Insert A[j] into the sorted sequence A[0..j - 1].
i = j - 1
while i > 0 and A[i] > key
A[i + 1] = A[i]
i--
A[i + 1] = key
시간 복잡도는 O(n^2)이다. 따라서 insertion sort 알고리즘이 절대 O(n^2)을 넘어서지 않는다. 공간 복잡도는 O(1)만큼 소요되고 추가 저장공간을 확보하지 않는다 (또 다른 알고리즘을 추가하지 않는 이상).
아래 깃허브 레포지토리에서 내가 Insertion Sort 알고리즘을 응용한 프로그램을 구현했다. 프로그램 내에 주석도 추가했으며 참고해도 좋을 것 같다.
yoonBot/Computer-Science-and-Engineering
Computer Science Engineering Notes and References from Textbooks and Lectures... Additional tutorials included - yoonBot/Computer-Science-and-Engineering
github.com
다음 글에서는 merge sort를 알아볼 예정이다. Merge sort는 Insertion sort랑 다르게 분할 정복 (Divide and Conquer) 메서드를 쓴다. 추가 비교들은 다음 글에 계시하도록 한다.
'알고리즘 저장소 (Algorithm Library) ⏱ > Sorting (정렬)' 카테고리의 다른 글
| Quick Sort (퀵 정렬) (0) | 2021.07.17 |
|---|---|
| Bubble Sort (거품 정렬) (0) | 2021.07.06 |
| Selection Sort (선택 정렬) (0) | 2021.07.04 |
| Merge Sort (합병 정렬) (0) | 2021.06.29 |
